
(1) Diffusion coefficient of lithium ions in LiCoO2
Taking the spherical electrode model to deal with the diffusion of lithium ions in the porous LiCoO2 electrode as an example, suppose:
① Each active material particle in the LiCoO2 electrode is treated with a spherical electrode;
②The electrode process is controlled by a potentiostatic step, and the step potential is very high, so the lithium ion concentration on the electrode surface after the step can be set to 0;
③Since the diffusion rate of lithium ions in the solid phase of LiCoO2 electrodes is much slower than that of liquid phase, the entire electrode process is controlled by the diffusion rate of lithium ions in the solid phase;
④ Taking the center of the sphere as the origin of the coordinate, the radial flow of each point on the sphere with a radius of r is:

r=r+dr The radial flow rate of each point on the spherical surface is:

In the formula, c is the concentration of lithium ions at the radius r in the LiCoO2 solid phase; DLi+ is the diffusion coefficient of lithium ions in LiCoO2 particles, as shown in Figure 1 and Figure 2.

Figure 1 - Schematic diagram of the electrode with LiCoO2 particles being spherically treated

Figure 2 - Schematic diagram of spherical diffusion
In the extremely thin spherical shell between the two spheres, the rate of change in the concentration of the reactive particles is:

Combining the above three formulas, the expression of Fick's second law in spherical coordinates can be obtained:

Initial conditions: when t=0, 0<r<r0, c(r,0)=c0
In the formula, r0 is the radius of the LiCoO2 particles; c0 is the concentration of lithium ions in the LiCoO2 particles before the start of the step.
Boundary conditions: when t>0, r=r0, c(r0, t)=0; when 0<t<τ, r=0, c(r,0)=c0.
In the formula, τ is the time for the boundary of the diffusion layer to extend to the center of the LiCoO2 particle after diffusion occurs.
Under the above initial and boundary conditions, solve the equation  , Obtain the expression of lithium ion concentration in LiCoO2 electrode:
, Obtain the expression of lithium ion concentration in LiCoO2 electrode:

Differentiate the above equation to r to get:

Substituting r=r0 into the above formula, we can get:
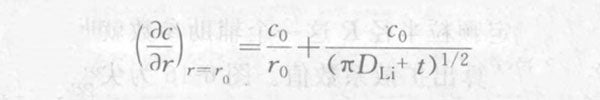
From this, the current response after the potential step is solved:

In the formula, n is the number of electrons gained or lost; F is the Faraday constant; A is the electrode area.
The above formula shows that there is a linear relationship between the current I of the test working electrode and t-1/2. Using this feature, the diffusion coefficient of lithium ions in LiCoO2 particles can be calculated. Rewrite the above formula as I=B+Kt-1/2.
among them,  .
.
The lithium ion diffusion coefficient DLi+ can be obtained from the two formulas B and K:

(2) Diffusion coefficient of lithium ions in LiMn2O4
According to the spherical diffusion model, the ratio of constant voltage to constant current charging capacity can be expressed as:

In the formula, ξ=R2/Dt, dimensionless; R is the particle radius, cm; t is the constant current charging time, s; D is the solid phase diffusion coefficient, cm2/s; αj is a constant sequence, which is solved by the equation tanα=α have to. The above equations are linearly fitted to ξ by the least square method in the range of different q values, and finally a series of equations of D=f(q) are obtained, as shown in Table 1. According to Table 1, as long as the particle radius R, constant voltage-constant current charging capacity ratio q and constant current charging time t are measured, the diffusion coefficient D can be obtained.
Table 1 - Equations for linear fitting by the least square method in different ranges of q values

Figure 3 The volumetric gap titration (CITT) curve measured in the first cycle. The t value can be obtained from the voltage versus time or current versus time curve in Figure 3(a), and the q value can be obtained from the voltage versus capacity curve in Figure 3(b). Therefore, the data obtained from the CITT curve can be obtained by measuring the particle radius R as an auxiliary parameter, and the diffusion coefficient value can be calculated from the equation in Table 1. Figure 4 shows the CITT curve of the first 20 cycles measured by the spinel LiMn2O4/Li battery, which has good stability. According to Figure 4, the diffusion coefficient of lithium ions in LiMn2O4 during the first 20 charging and discharging processes is calculated as shown in Figure 5. It can be seen from Figure 5 that the solid-phase diffusion coefficient of lithium ions in LiMn2O4 is not only related to the voltage or the concentration of lithium ions in the Mn2O4 lattice or the depth of charge (DOC), but also the diffusion coefficient changes significantly during the charging cycle. . As the voltage changes, there are two extremely small peaks around 3.95V and 4.12V, and the entire diffusion coefficient voltage curve is in a twisted "W" shape.

Figure 3 - The first CITT curve of spinel LiMn2O4 measured under constant current charging current

Figure 4 - The first 20 CITT curves of spinel LiMn2O4

Figure 5 - The first 20 lgD-E curves of lithium ion in LiMn2O4
Using volumetric intermittent titration technology can easily detect the diffusion coefficient of intercalated ions in the electrode material under different voltages and different number of charge and discharge cycles.
(3) Diffusion coefficient of lithium ions in graphite
In the potential step interval, assuming that the lithium ion diffusion coefficient does not change with its concentration in the electrode material, after the potential step, the diffusion of lithium ions in the spherical electrode material conforms to Fick's second law. After derivation, the relationship between response current i and time t can be obtained:

The applicable condition of this formula is t≪R2/D. Where i(t) is the response current after the potential step; S is the surface area of the spherical particle; F is the Faraday constant; D is the lithium ion diffusion coefficient; c0 and ca are the lithium ion concentration before and after the potential step; R is the particle radius. According to the above formula, the response current i(t) and t-1/2 satisfy a linear relationship in a short time. From this relationship, the lithium ion diffusion coefficient can be obtained.
It is assumed that the molar volume of the graphite material is Vm, which does not change with the change of the lithium ion concentration. The relationship between the surface area and volume of 1 mol material is 
. The relationship between the amount of electricity ΔQ (mA·h) flowing through the step interval and the change in lithium ion concentration is ΔQ=0.2778ncFVm(ca-c0), and nc is the amount of graphite in the pole piece. Assume that m (mA·s1/2) is the slope of the linear relationship between response current i and t-1/2. After deduction, the calculation expression of the lithium ion diffusion coefficient in the graphite anode material with a radius of R (cm) is:

In fact, the shapes of graphite material particles are various, even graphitized mesophase carbon pellets (MCMB) will not have a perfect spherical shape. Considering the actual shape of the particles, the specific surface area measured by the BET method is generally used to calculate the lithium ion diffusion coefficient.
A more reliable value can be obtained by calculating the true specific surface area S of the material by electrochemical method and calculating the lithium ion diffusion coefficient. The relationship between the deduced lithium ion diffusion coefficient and the real specific surface area Se (cm2/g) and density ρ (g/cm3) is:

















