
During the charging and discharging process of lithium ion batteries, the main electrode reaction is the insertion and extraction of lithium ions in the positive or negative electrode materials. Therefore, the diffusion coefficient of lithium ions in the positive and negative electrode materials is an important indicator. In electrochemical tests, according to Fick’s second law, a variety of methods can be used to determine the diffusion coefficient of ions, such as steady-state cyclic voltammetry, rotating disk electrode method, transient potentiostatic step method, constant current step method, AC impedance method, etc. For lithium-ion batteries, commonly used electrochemical testing methods include current pulse relaxation (CPR), constant current intermittent titration (GITT), alternating current impedance method (AC), and potential step method (PSCA). In the research of lithium-ion batteries, some of the above-mentioned methods involve the determination of the open circuit voltage (OCV) and the slope of the composition curve, and some methods involve the determination of the effective surface area of the electrode, and the determination of these parameters is sometimes difficult, and even brings great errors, resulting in a large difference between the measured diffusion coefficient and the actual value, which sometimes reaches several orders of magnitude.
The electrochemical diffusion coefficient of lithium ions inside the crystal can be calculated by Weppner and Huggins method, and the chemical diffusion coefficient  is expressed as:
is expressed as:

In the formula, j is the current density; Vm is the molar volume of the sample; F is the Faraday constant; dE/dx is calculated by Coulomb
The titration curve is obtained; dE/dt1/2 is obtained from the relationship between voltage and time under constant current conditions.
Several test methods of diffusion coefficient are introduced as follows.
(1) Current pulse relaxation method (CPR)
The current pulse relaxation method is to impose continuous constant current perturbation on the electrode, record and analyze the potential response after each current pulse. This method can be used to determine the diffusion coefficient of lithium ions in a lithium ion battery. When each pulse current applied to the battery ends, the voltage of the battery returns to the potential before the pulse starts, and its changing law is:
U=f(t -1/2)
The change in battery voltage can be expressed as:

According to Fick's second law, for a planar electrode under semi-infinite diffusion (t≤l2/DLi), its chemical diffusion coefficient can be expressed as:

In the formula, I is the pulse current, A; τ is the pulse time, s; Vm is the molar volume, cm3/mol; A is the cathode or anode surface area, cm2; F is the Faraday constant; t is the time, s;
l is 1/2 of the electrode thickness; dU/dx is the slope of each point on the discharge voltage composition curve; dU/dt-1/2 is the slope of the relaxation potential (dU or ΔU)-t -1/2 line.
(2) Alternating current impedance technology (AC)
AC impedance technology is an important method in electrochemical research and has been widely used in various battery research. An important feature of this technology is that it can accurately distinguish the electrode process speed decision steps in different frequency ranges based on the impedance spectrogram (Nyquist diagram or Body diagram).
Under the condition of semi-infinite diffusion, the Warburg impedance can be expressed as:
ZW = σω-1/2 - jσω-1/2
In the formula, σ is the Warburg coefficient; ω is the angular frequency; j= .
.
When the frequency ≫ 2DLi/l2, the Warburg coefficient is:

In the formula, l is the diffusion thickness; the meaning of Vm, F, A, dU/dx is the same as the formula in the current pulse relaxation method.
According to the Warburg coefficient of the measured impedance spectrogram, combined with the dU/dx under different lithium insertion amounts measured by the discharge potential-composition curve, the diffusion coefficient DLi can be obtained.
(3) Constant current intermittent titration technology (GITT)
Constant current intermittent titration technology is a combination of steady-state technology and transient technology. It eliminates the problem of ohmic potential drop in constant potential technologies, and the data obtained is accurate.
In Figure 1, ΔUt is the total transient potential change of the constant current I0 during the time τ, and ΔUs is the steady-state voltage change of the battery caused by the application of I0. The current of the battery through I0, during the time τ, lithium is embedded in the electrode, which causes the concentration of lithium in the electrode to change, according to Fick's second law:

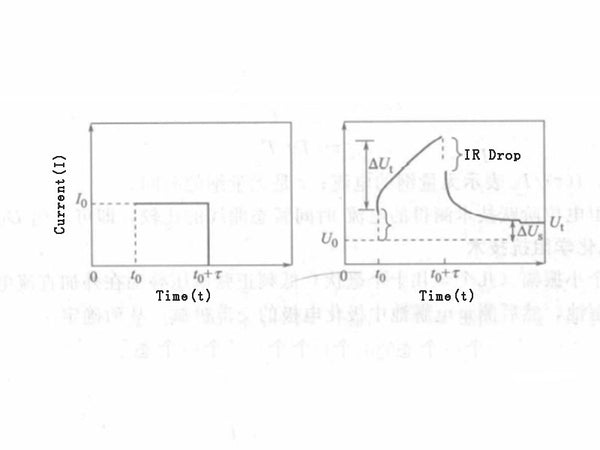
Figure 1 - Current (a) and voltage (b) changes with time in constant current gap titration
The initial conditions and boundary conditions are:

In the formula, x=0 represents the electrode/solution interface, and other parameters are the same as described above. When t≤l2/DLi, dU/dx is the slope of the open circuit potential-composition curve, and the meaning of other parameters is the same as before. According to the U-t relationship curve under constant current, the diffusion coefficient DLi can be obtained.
(4) Electric order technology (PSCA)
The potential step technique (PSCA) is a commonly used transient research method in electrochemical research. The diffusion coefficient can be calculated according to the I-t1/2 relationship curve after the step and the Cottrel equation.
Kanamura and Uchina et al. used this technology to measure the diffusion coefficient of the intercalation process in the positive and negative electrode materials of lithium-ion batteries. That is, at a certain potential and within a constant time, the lithium ions in the electrode are diffused to a uniform state, and then a potential step signal is given from the potentiostat, there is a transient current in the battery. Record the change of transient current with time during this potential step. DLi can be obtained according to the recorded current-time transient curve and the theoretically calculated current-time transient curve. The theoretically calculated time-current transient curve can be derived from Fick's second law:

In the formula, DLi is the diffusion coefficient of lithium ions in the electrode. Assuming that the electrode thickness is l, the initial conditions and boundary conditions are:

From the above initial conditions and boundary conditions, the theoretical time-current transient curve can be solved as:

In the formula, I(τ)/I∞ represents the dimensionless current; τ is the dimensionless time.
DLi can be obtained by comparing the current-time transient curves measured by the potentiostatic step technique.

















