main content:

  • 1. Lithium insertion thermodynamics
  • 2. Free energy changes during the lithium intercalation reaction
  • 3. Partial molar entropy and partial molar enthalpy of lithium insertion

    •  

    1.Lithium insertion thermodynamics

     

    The discharge mechanism of Li/LixMn2O4 (0<x<2) battery is the electrochemical intercalation reaction of lithium in [Mn2O4]. The overall battery reaction is expressed as:
    xLi+[Mn2O4]⇌LixMn2O4

     

    In the embedding reaction, the electromotive force of the battery changes with the embedding depth x, so the change of the free energy of the battery reaction should take the integral form of the electromotive force:
    △Gin=-nF∫x0E(x)dx

     

    The embedded partial molar entropy ΔS~in and partial molar enthalpy ΔH~in are respectively:
    △S~in=F(əE/əT)x
    ΔH~in=F[(əE/əT)x-E]

    2. Free energy changes during the lithium intercalation reaction

    Figure 1 shows the Coulomb titration curve [EMF(x)] of Li/LixMn2O4 battery at 30℃. In the interval of 1<x<2, the voltages are respectively 4.1V, 3.95V and 2.97V, showing three platforms, which are all higher than the battery electromotive force calculated according to the conventional redox reaction.

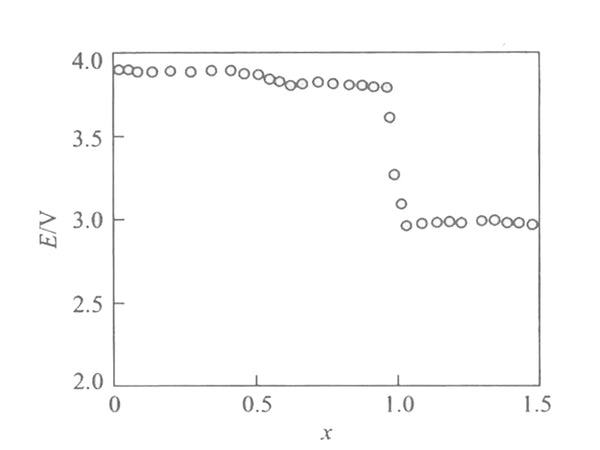
    Figure 1 EMF(x) curve of Li/LixMn2O4 battery at 30℃

     

    With [Mn2O4] as the cathode material, the Li/LixMn2O4 battery is fully discharged, and the final product of the cathode will be Mn and Li2O. The whole reaction can be expressed as:
    8Li+[Mn2O4]→4Li2O+2Mn

     

    According to the thermodynamic calculation of the traditional oxidation-reduction reaction, the free energy of the reaction becomes -1313k/mol; if this reaction is realized electrochemically, the free energy of the reaction can be obtained by integrating the EMF(x) curve over the entire discharge interval, and the calculated value It is -1248kJ/mol. This change value is quite consistent with the calculation result of the above formula, so it can be considered that the intercalation reaction of lithium in [Mn2O4] is an intermediate process of the whole reaction, that is, the high electromotive force when x<2 is the total energy of the above reaction The result of redistribution in the various processes of the reaction. This is because if the reaction proceeds according to the above formula, it will inevitably involve the destruction of the [Mn2O4] lattice and the formation of the Li2O lattice, which requires energy absorption, and the insertion of lithium in [Mn2O4] Since the reaction does not involve the destruction and formation of the crystal lattice, the loss of lattice energy is avoided.

    3. Partial molar entropy and partial molar enthalpy of lithium insertion

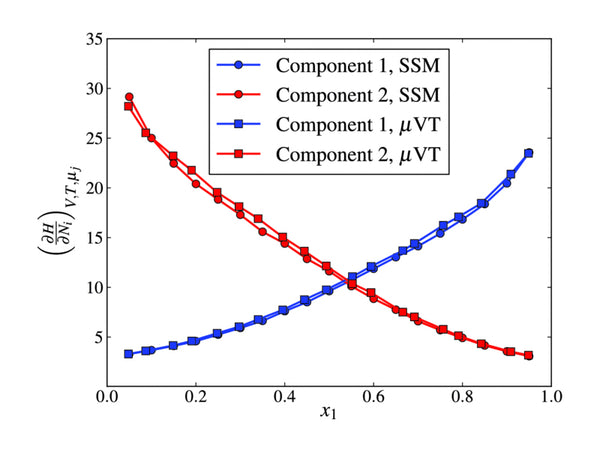
    Figure 2 shows the EMF(x) curves of Li/LixMn2O4 batteries with different embedding depths at different temperatures.

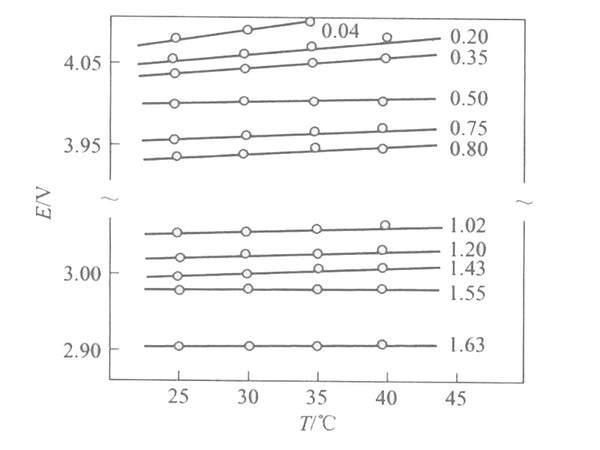
    Figure 2 EMF (x) curves of Li/LixMn2O4 batteries with different embedded depths at different temperatures

     

    According to the formula ΔH~in=F[(əE/əT)x-E], the partial molar fan at different embedding depths is shown in Figure 3. It is reported in the literature that when the embedding depth is relatively small (x<0.1), the partial molar entropy of the embedding reaction is very large, about 60-100J/(mol·K). It reflects that lithium has a large degree of freedom and high fluidity in the [Mn2O4] lattice. When x increases, the partial molar entropy decreases. In addition, there are two minima at x=1/2 and x=1, indicating that the embedding process has changed when x=1 and x=1/2. From the structure analysis of LixMn2O4 (0<x<2), it can be seen that when x=1, the position of the tetrahedron 8a is already occupied, and if there is more lithium intercalation at this time, it will inevitably enter the position 16c of the octahedron. At this time, the crystal structure of [Mn2O4] changes from cubic crystals to tetragonal crystals, and the space group changes from Fd3m to F41/ddm, which leads to a huge change in the embedded partial molar entropy, and the minimum value at x=1/2 is and [Mn2O4] The superstructure of the lattice is related, that is, there is a sub-lattice problem. At this time, the entire crystal appears to be in a long-range order and no longer in a short-range order. It happens that one sub-lattice is full and the other is completely empty, macroscopically It appears that when x=1/2, the unit cell parameters have a sudden jump.

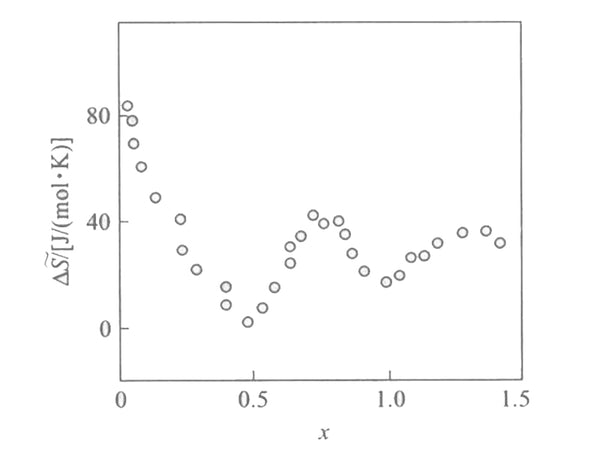
    Figure 3 Relationship between partial molar entropy and embedding depth

    According to the EMF(x) curve and the partial molar entropy data, the relationship between the partial molar enthalpy and the insertion depth of the lithium intercalation reaction in [Mn2O4] can be obtained, as shown in Figure 4. It can be seen that the bond and force between lithium and [Mn2O4] lattice is very strong, and the partial molar enthalpy has a maximum value when x=1/2 and x=1. The partial molar melting value at x<1 is very different from that at x>1, reflecting that lithium has entered two different lattice positions.

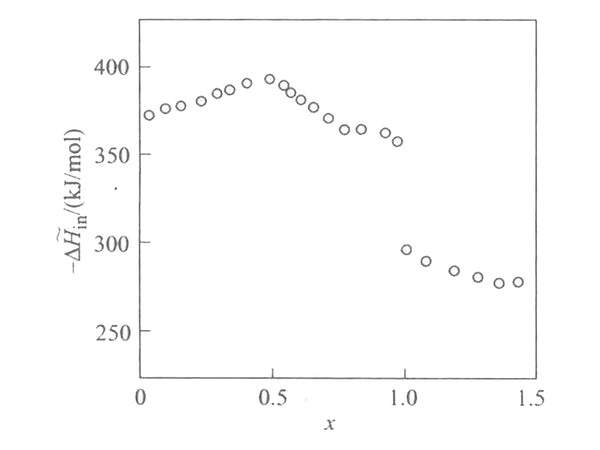
    Figure 4 The relationship between embedding partial molar enthalpy and embedding depth