The AC impedance method can be used to determine the surface film impedance of the negative electrode material and the diffusion coefficient of lithium ions in it. Lithium ions are inserted into the carbon electrode, and the SEI passivation film is first formed on the surface of the electrode, so the equivalent circuit of lithium insertion can be shown in Figure 1. The equivalent circuit consists of two parts: one part reflects the SEI passivation film; the other part reflects the electrochemical reaction of the carbon electrode and the diffusion of lithium ions in the electrode. R0 is the resistance of the solution, and Rc and Rf are the Faraday impedance and the SEI film impedance, respectively. W is the War-burg impedance, that is, the impedance caused by the diffusion of lithium ions in the carbon electrode; Cd and Cf are the capacitances corresponding to Rc and Rf, respectively.
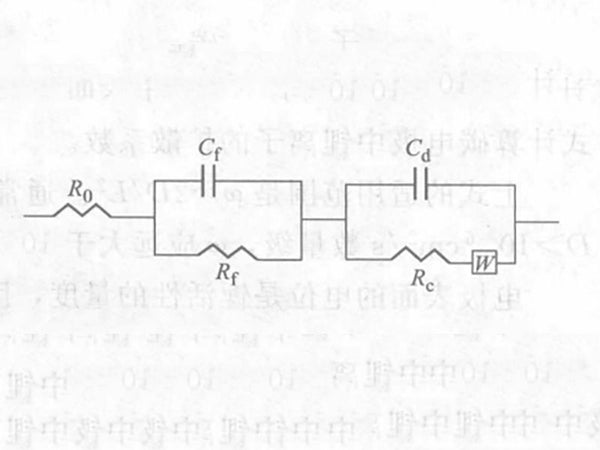
Figure 1 - Equivalent circuit diagram of lithium ion inserted into carbon anode material
Since W is a function of frequency and Rc is not, the reaction rate of the electrode is controlled by the diffusion of lithium ions in the electrode at low frequency (long time), and by electrochemical reaction at high frequency (short time). Studies have shown that: only at a lower frequency (shorter time) than the corresponding electrochemical reaction control, the electrode reaction rate is controlled by the transfer of the passivation film SEI.
For semi-infinite diffusion and finite diffusion, the Warburg impedance W is determined by the following formula:
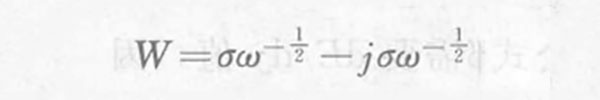
In the formula, ω is the AC angular frequency; σ is the Warburg coefficient.
When a small AC voltage is applied to the electrode, assuming that the electrode is a flat electrode, the diffusion of lithium ions in the carbon electrode is a one-dimensional diffusion within the thickness of the electrode, and the diffusion satisfies Fick's second law. After a series of mathematical derivations,
The phase difference between the current and the voltage is 45°, which has nothing to do with the angular frequency, so the Warburg coefficient is as follows:
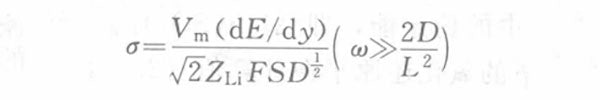
In the formula, Vm is the molar volume of carbon electrode LiyC6 stoichiometrically calculated at y=0; ZLi is the number of electrons transported by lithium ions, 1; S is the cross-sectional area between the electrolyte and the electrode; F is the Faraday constant; D is the chemical diffusion coefficient of lithium ions in the electrode; dE/dy is the slope of the stoichiometric y of the LiyC6 coulometric titration curve; ω is the AC angular frequency; L is the electrode thickness. The diffusion of lithium ion concentration is reflected in the complex plane diagram of the electrode impedance as a 45° straight line, as shown in Figure 2.
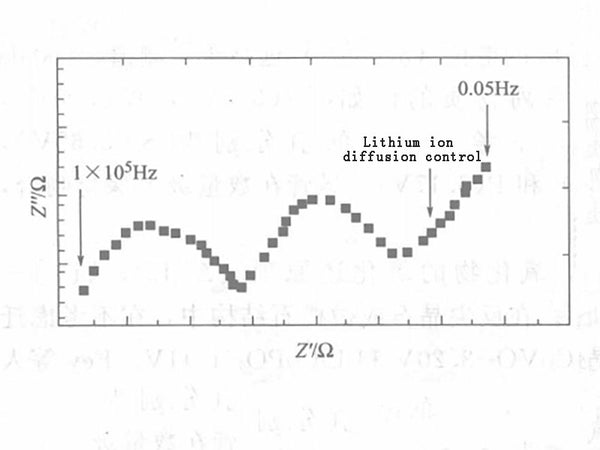
Figure 2 - Complex plan view of the negative electrode impedance of a lithium-ion battery
Lithium-intercalated carbon materials, especially graphite, etc., will have some voltage plateaus on the coulometric titration curve, making it difficult to obtain dE/dy accurately. In order to avoid using the dE/dy value, a certain transformation process is performed on the above equation, and the following Warburg coefficient equation is obtained:
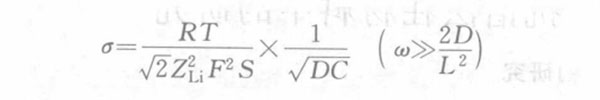
In the formula, C is the concentration of lithium in the electrode, that is, the stoichiometric y molar volume Vm of the carbon electrode LiyC6 (the molar volume of the carbon electrode LiyC6 stoichiometric y=0); ZLi is the number of lithium ion transported electrons, 1; S is the cross-sectional area between the electrolyte and the electrode; F is the Faraday constant; R is the gas constant; T is the thermodynamic temperature. The above formula can be used to calculate the diffusion coefficient of lithium ions in the carbon electrode.
The applicable range of the above formula is ω≫2D/L2, usually the electrode thickness L is on the order of 10-2cm, the diffusion coefficient D>10-6cm2/s, and the ω should be much larger than 10-2Hz. The actual measurement of ω can meet this requirement. assumed:
The potential of the electrode surface is a measure of lithium activity, so the electrode should be mainly an electronic conductor;
The driving force of diffusion is only the chemical gradient, and the electric field is negligible, so the electrode should have high conductivity;
The system is linear, that is, within the range of applied AC voltage, the diffusion coefficient has nothing to do with the concentration. In addition, The processing of formula ![]()
assumes that the system has no concentration polarization, so the actual applied voltage should be very small, and the measured impedance has nothing to do with the voltage amplitude.
In addition to the above assumptions, there are also problems with the approximate treatment of the molar volume of the electrode, the area of the interface between the electrolyte and the electrode, and the influence of the electrode manufacturing method.
After processing, the Warburg coefficient formula part needs dE/dy value, so the AC impedance method can measure the diffusion coefficient of lithium ions in all carbon materials. The AC impedance method can provide more electrode information by applying the complex plane graph method. Figure 1 reflects the entire electrode process of lithium insertion into the carbon electrode, and the relevant parameters that can be obtained: such as the resistance of the solution, the Faraday impedance, the impedance of the SEI film, and the corresponding capacitance.
















