main content:
1. Battery heat production and rate calculation
For a dual electrolyte battery, ignoring the influence of the mixing enthalpy change and the phase transition process, the total heat production of the battery can be expressed as
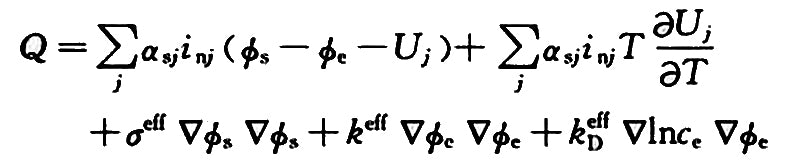
where αsj is the interface area per unit volume, cm2·cm-3; inj is the transfer current density, A·cm-2; Фs is the substrate potential, V; Фe is the solution potential, V; Uj is the equilibrium potential, V; T is the temperature, K; σeff is the effective conductivity of the matrix, Ω-1·cm-1; ce is the electrolyte concentration, mol·cm-3.
It can be seen that the calculation of the above formula is more complicated. In order to simplify the calculation, the reaction heat of the battery is represented by Qr; the energy loss caused by the polarization of the battery is represented by Qp; there are side reactions in the battery, the typical side reactions are the decomposition and self-discharge of the electrolyte, and the energy loss caused by the side reactions It is represented by Qs; there is resistance in the battery, which produces Joule heat Qj. Therefore, the total heat source of a battery can be expressed as
Q=Qr+Qp+Qs+Qj
Average battery heat production rate (W) = heat generated (J) / cycle time (s)
Mathematically expressed as
V=Q/t
In the formula, V is the average heat production rate, W; Q is the total heat production of the battery during the working time of the battery, J; t is the working time of the battery, s.
The heat generation of the battery is related to its own properties, including the following parts:
(1) The chemical composition and structure of the battery.
(2) The initial state and termination state of the charge.
(3) The initial temperature of the battery.
(4) Rates and modes of charging and discharging.
When the battery type is determined, it is necessary to investigate the effects of (2) to (4) above, and design experiments to measure and calculate. For example, a battery module is discharged from 100% state of charge (SOC) to 0% state of charge at 1C, and the cycle time is 3600s. The heat generation rate can be calculated after measuring the heat released by the process.
The energy efficiency of the battery during charge, discharge or charge-discharge cycles can also be determined by measuring the heat generation rate of the battery.
Energy efficiency = [1-(heat generated by battery/electric energy input or output)]×100
Mathematically expressed as
H=(1-Q/E)×100
To design a thermal management system, in addition to knowing the heat generation rate of the battery, it is also necessary to know the heat capacity of the battery. Heat capacity refers to the energy required to heat or cool 1kg of battery material to raise or lower it by 1°C, and the unit is J·kg-1·°C-1. According to the calorimetric method to obtain the heat Q lost or obtained by the battery module changing from the initial temperature T1 to the final temperature T2, the heat capacity of the battery is
Cp=Q/m (T1-T2)
where m is the total mass of the battery module.
2. Diffusion of battery heat

There are three basic ways of transferring heat energy: heat conduction, heat convection and heat radiation. The heat dissipation of Li-ion power batteries includes these three heat transfer methods, and different heat dissipation technologies focus on certain specific methods. The thermal radiation mainly occurs on the surface of the battery, which is related to the properties of the material on the surface of the battery. It is expressed by the Stefan-Boltzmann law as
Pr(T)=εσ(T4-T4S)
In the formula, Pr is the radiation power; ε is the thermal emissivity, for a black body, ε=1; σ is the Stefan-Boltzmann constant, that is, the black body radiation constant; T is the battery temperature, K; Ts is the ambient temperature, K.
Heat conduction mainly includes the heat transfer between various substances inside the battery, such as the electrode, electrolyte, current collector, etc. of the battery, that is, the battery is taken as a whole, and the heat is transferred from the inside of the battery to the surface of the battery, which is expressed by Fourier's law.
qn=-k (əT/ən)
In the formula, qn is the heat flux density, W·m-2; k is the thermal conductivity, W·m-1·K-1; əT/ən is the temperature gradient in the normal direction of the electrode isotherm, K·m-1.
Thermal convection means that the heat on the current surface exchanges heat through the flow of heat exchange media (such as air, water, etc.), which is proportional to the temperature difference, and is expressed by Newton's formula as
Q=hA(Tm-Tf)
where Q is the heat flux, W; h is the convective heat transfer coefficient, W·m-2·K-1; A is the area, m2; Tm is the wall temperature, K; Tf is the fluid temperature, K.
For Li-ion power batteries, the heat radiation and heat convection inside the battery have little influence, which is mainly determined by heat conduction. The heat absorbed by the battery itself depends on the specific heat capacity of the battery material, and the temperature rise of the battery is inversely proportional to the specific heat capacity of the battery material itself.
Table 1 shows the heat production qT of the 18650 type (capacity 1.35A h) Li-ion battery at different discharge rates and the heat dissipation qd at different operating temperature ranges, where qacc is the heat absorbed by the battery itself. It can be seen that the heat of the battery is used to increase its own temperature because the heat dissipation is not timely, resulting in an increase in qacc. Therefore, through the heat dissipation of the battery, increasing the value of qd and decreasing the value of qacc can reduce the internal working temperature of the battery.
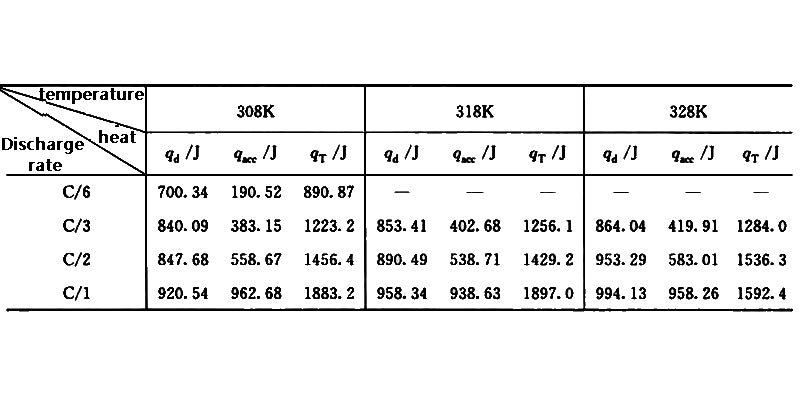
Table 1 Heat generation and heat dissipation behavior of 18650 Li-ion battery

















